Aplicação de números complexos

  Aplicação de números complexos

 

   Os números complexos apareceram no século XVI ao longo das descobertas de procedimentos gerais para resolução de equações algébricas de terceiro e quarto grau. No século XVII os complexos são usados de maneira tímida para facilitar os cálculos. No século XVIII são mais usados na medida que se descobre que os complexos permitem a conexão de vários resultados dispersos da Matemática no conjunto dos números reais. No entanto, nada é feito para esclarecer o significado desses novos números. No século XIX, aparece a representação geométrica dos números complexos, motivada pela necessidade em Geometria, Topografia e Física, de se trabalhar com o conceito de vetor no plano. Os números complexos passam a ser aplicados em várias áreas do conhecimento humano, dentro e fora da Matemática.

     A primeira aplicação de números complexos à teoria de circuitos elétricos parece ter sido realizada pelo cientista alemãoHermann von Helmholtz (1821-1824). A aplicação de números complexos na análise de circuitos elétricos de corrente alternada (CA) foi disseminada nos Estados Unidos por Arthur Edwin (1861-1939) e Charles Steinmetz (1865-1923) com auxílio de Julius Berg (1871-1941) no final do século XIX. Em 1823, Edwin adotou o termo Impedância (inventado porHeaviside) assim como os números complexos para os elementos dos circuitos elétricos CA, o que foi seguido por Steinmetz. Desde então, os números complexos são fundamentais para a Engenharia Elétrica

    Em circuitos de corrente alternada, por exemplo, as instalações elétricas residenciais, as grandezas elétricas são analisadas com o auxílio dos números complexos, o que facilita muito os cálculos.

 

  Veja algumas aplicações de números complexos

 

Números Complexos e a Física

 

    Há mais de 200 anos, a física e a matemática estão intimamente ligadas no que diz respeito a conjuntos numéricos.
Embora não haja um estudo mais aprofundado, já se sabe que atualmente, na física contemporânea, a aplicação do conjunto dos números complexos é tão grande, que é até possível pensar em uma autêntica " complejificación de la física", como cita o autor Frederico de Rubio y Galy em "The Role of Mathematics in the Rise of Science".
Nesta mesma obra, Dr Frederico dá aos números complexos a idéia de par ordenado: " um par ordenado de números reais, onde suas coordenadas representam a parte real e imaginária do complexo". Assim, apresenta como os números complexos podem multiplicar-se e como é simples a sua representação como vetor.
Fica claro então, como o universo de complexos se expande no mundo da física, onde é utilizado pelos físicos contemporâneos de forma familiar em diversas teorias. Vejamos alguns exemplos.
 
 

Vetores e Quantidades Complexas

 

   Dado um número complexo determinado por ( a,b ), onde a e b são números reais, podemos facilmente representa-lo em um plano. Tomando como base a localização de pares ordenados, localizamos o par ( a,b ) e formamos o vetor com origem em ( 0,0 ) e extremidade em ( a,b ).
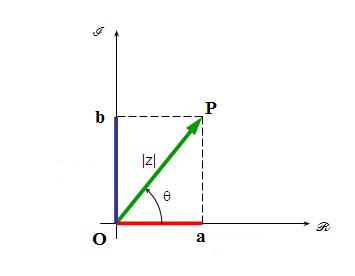
     Para facilitar essa representação, vamos utilizar uma nova quantidade que chamaremos de operador i, embora alguns autores também o denominam operador j. Observemos a figura:

Figura I




     O vetor H, representado sobre o eixo de referência, à direita do eixo vertical está sofrendo uma rotação. Ao se deslocar para a esquerda do eixo vertical, temos o vetor – H , que é o próprio vetor H multiplicado por –1. Então, se para fazer com que o vetor gire 180° é necessário multiplica-lo por –1, para que sua rotação seja de 90° ( e o vetor se localize sobre o eixo vertical ) é necessário multiplica-lo por , pois . = -1.
    A expressão  não é aceita como número real e é então simbolizada pela letra i. Assim, qualquer vetor multiplicado por i, sofre uma rotação de 90° .
Portanto, na figura anterior temos:

Figura II

    Esta representação onde o vetor acompanhado de +i está no eixo vertical para cima e acompanhado de –i está no eixo vertical para baixo é chamada forma complexa.
 
 

Números complexos e circuitos monofásicos

 

     No estudo de circuitos, a aplicação de números complexos aparece na forma de vetores, que determinam algumas equações importantes, com a presença da unidade imaginária.
Um circuito monofásico é alimentado por uma única tensão alternada. Quando a única dificuldade que a tensão sofre é a resistência efetiva, o circuito é dito puramente resistivo. Nesse circuito, a tensão Er e a intensidade de corrente I atingem valores correspondentes ao mesmo tempo, o que faz com que os seus vetores representativos fiquem sobre o eixo de referência. Dizemos então que as grandezas estão em fase.
 
 

Figura III
 
 

Figura IV




     Quando a dificuldade que a corrente sofre é a reatância capacitiva, o circuito é chamado puramente capacitivo. Nesse circuito, Ec e I não atingem valores correspondentes ao mesmo tempo, de modo que os vetores que as representam fiquem um sobre cada eixo. Neste caso, dizemos que Ec e I estão defasadas 90° ( I se antecipa aos valores de Ec ).
 
 

Figura V
 
 

Figura VI

      Quando o circuito apresenta como dificuldade à reatância indutiva, o circuito é chamado de puramente indutivo. Nesse circuito Ei e I também estão defasadas 90° (I está atrasada aos valores de Ei).

Figura VII
 
 

Figura VIII

Circuito em fase tipo R –C

 

    R e C simbolizam a resistência e a capacitância equivalente. Nesse circuito, a dificuldade encontrada pela fonte para estabelecer uma corrente no circuito é determinada pela soma vetorial de R e X_c.A tensão E é a soma vetorial das componentes Er e Ec.

Figura IX      Observa-se que o ângulo de defasagem é menor que 90° , assim, podemos representar o vetor E na forma trigonométrica, onde E = E cos q - i sen q ou na forma binômia E = Er – i Ec. 

Circuito em série tipo R – L – C

 

     Neste tipo de circuito três situações podem ocorrer:

Figura X




    No primeiro caso, o circuito comporta-se como circuito indutivo, o segundo como capacitivo e o terceiro como resistivo.
Nesse caso o vetor é representado na forma E = Er + i ( El – Ec ) = E cos q + i sen q .
 
 

Números complexos e sinais sinusoidais

 

   Além das formas trigonométrica e binômia, os números complexos podem ser representado em notação exponencial, onde Z = P e ^iq, sendo P o módulo do complexo e q o ângulo formado com o eixo de referência ( argumento ).
  Esta propriedade dos complexos é muito utilizada para expressar as funções seno e cosseno em notação exponencial, onde:
cos ( x) = 
sen (x) = 
    Assim, podemos representar as exponenciais complexas:
e ^{i (x)} = cos (x) + i sen (x)
e ^{–i (x)} = cos (x) - i sen (x)
   Com isso, a resolução de uma equação com funções sinusoidais pode ser efetuada recorrendo a uma função exponencial complexa. 

Números complexos e a função de onda

 

    A equação de onda que rege o movimento dos elétrons foi obtida por Schrodinger em 1925. Esta equação é análoga a equação de onda clássica e o que a difere é justamente a aparição explícita do número imaginário i.. Vejamos

    Vemos que essa equação é satisfeita pela função de onda harmônica, que nada mais é que um complexo em sua forma polar:

  As funções de onda de Schrodinger não são necessariamente reais, contudo a probabilidade de encontrar um elétron é totalmente real. Para podermos encontrar essa probabilidade, mudaremos a interpretação da equação de onda de modo que ela seja real.     Para isso, utilizaremos a propriedade que o complexo possui de, quando multiplicado por seu conjugado, se tornar real. Assim, a probabilidade será dada por:
, onde é o conjugado do complexo 
 
 
   Esta equação é chamada de equação de normalização. Essa condição tem um papel importante na mecânica quântica, pois coloca uma restrição nas soluções da equação de Schrodinger que leva à quantização de energia.
    Com os aspectos abordados acima, percebemos que o conjunto de números complexos tem um universo infinito de aplicações, que com a Física Moderna e descobertas recentes está aumentado cada vez mais. A exposição dessas aplicações no ensino médio deve ser feita de maneira simples e superficial, visto que nossos alunos não possuem muitos dos conhecimentos aqui abordados, mas o certo é, que não podemos priva-los desse entendimento.
   Atualmente, o ensino da matemática em geral deve procurar trabalhar com exemplos práticos, na vida e em outras disciplinas (trabalhar a interdisciplinaridade), para despertar no aluno à vontade e o desejo de aprender. Com isso, qualquer assunto ou tópico construirá um conhecimento sólido e não superficial e os alunos conseguirão estabelecer relações mais facilmente.
 
 
 

Algumas questões de números complexos

Teste seus conhecimentos!!!

   1. (UFU-MG) Sejam os complexos z = 2x – 3i  e  t = 2 + yi, onde x  e  y são números reais. Se z = t, então o produto x.y é

     A) 6       B) 4       C) 3       D) –3       E) –6 

   2. (PUC-MG) Qualo é o quociente de (8 + i)/(2 - i) é igual a

     A) 1 + 2i       B) 2 + i       C) 2 + 2i       D) 2 + 3i       E) 3 + 2i 

   3. (UFV-MG) Dadas as alternativas abaixo

I.  i² = 1        II. (i + 1)² = 2i         III. ½4 + 3i½ = 5       IV. (1 + 2i).(1 – 2i) = 5 pode-se dizer que

A) todas as alternativas acima estão corretas

B) todas as alternativas acima estão erradas

C) as alternativas I e III estão erradas

D) as alternativas II, III e IV estão corretas

E) as alternativas I e III estão corretas 

   4. (MACK-SP) Se I é um número complexo e Ī o seu conjugado, então, o número de soluções da equação Ī = I² é:

A) 0       B) 1       C) 2       D) 3       E) 4 

  5. (ITA-SP) Os complexos u e I, de módulo igual a 1, são representados no plano de Argand-Gauss por dois pontos simétricos em relação ao eixo real. Vale então a relação

A) u. Ī = 1         B) u. I = 1       C) u + Ī = 0       D) u. I = 0       E) n.r.a 

   6. (CESGRANRIO-RJ) O módulo do complexo z, tal que z² = i, é

A) 0       B) (Ö2)/2       C) 1       D) Ö2       E) 2 

   7. (UFPA-PA) Qual o valor de m, real, para que o produto (2 + mi).(3 + i) seja um imaginário puro?

A) 5       B) 6       C) 7       D) 8       E) 10 

   8. (MACK-SP) O conjugado de (2 - i)/i vale

A) 1 – 2i       B) 1 + 2i       C) 1 + 3i       D) –1 + 2i       E) 2 - i 

    9. Se n é um inteiro, então o conjunto solução em Z, da equação iⁿ + i^-n = 0, onde i = Ö-1, é:

A)	{n Є Z/ n é ímpar}
B)	{n Є Z/ n é par}
C)	{n Є Z/ n > 0}
D)	{n Є Z/ n < 0}
E)	Z

   10. (UFPA-PA) Qual o valor de m, real, para que o produto (2 + mi).(3 + i) seja um imaginário puro?

A)  5       B)  6       C) 7       D) 8      E) 10

   11. Calcule o número complexo i¹²⁶ + i^-126 + i³¹ - i¹⁸⁰

 

   12. Sendo z = 5i + 3i² - 2i³ + 4i²⁷ e w = 2i¹² - 3i¹⁵ , calcule Im(z).w + Im(w).z . 

   13. (UCMG) O número complexo 2z, tal que 5I + Ī = 12 + 6i é:  

   14. (UCSal) Para que o produto (a + i).(3 - 2i) seja real, a deve ser: 

   15. (UFBA) Sendo a = -4 + 3i , b = 5 - 6i  e  c = 4 - 3i , o valor de ac + b é:

   16. (Mackenzie-SP) O valor da expressão y = i + i² + i³ + ... + i¹⁰⁰¹ é: 

   17. Determine o número natural n tal que (2i)ⁿ + (1 + i)²ⁿ + 16i = 0.

   18. Calcule [(1 + i)⁸⁰ + (1 + i)⁸²] : i⁹⁶.2⁴⁰

   19. Se os números complexos z e w são tais que z = 2 - 5i e w = a + bi, sabendo-se que z + w é um número real e  z.w .é um imaginário puro , pede-se calcular o valor de b² - 2a.

   20. Se o número complexo z = 1 - i é uma das raízes da equação x¹⁰ + a = 0, então calcule o valor de a.

   21- Determine o número complexo I tal que iI  + 2.Ī + 1 - i = 0. 

  22. (UFMG) Se z = (cos q + i senq)  é um número complexo na forma trigonométrica, mostra-se que zⁿ = rⁿ(cos q + i sen nq) para todo n Î IN. Essa fórmula é conhecida como fórmula de De Moivre. 

A) Demonstre a fórmula de De Moivre para n = 2, ou seja, demonstre que z² = r²(cos 2q + i sen 2q).

B) Determine todos os valores de n, n Є IN, para os quais  (Ö3 + i)ⁿ  seja imaginário puro. 

   23. (UFMG) 

A) Dado o número complexo na forma trigonométrica I = 2[cos (3p/8) + i sen(3p/8)], escreva os números complexos Ī, I² e na forma trigonométrica.

B) No plano complexo da figura abaixo, marque e identifique os números I, Ī, I² e no item acima.

 

Nessa figura, os ângulos formados por dois raios consecutivos quaisquer têm a mesma medida.

   24. (UFMG) Por três pontos não-colineares do plano complexo, z₁, z₂ e z₃, passa uma única circunferência.

Sabe-se que um ponto z está sobre essa circunferência se, e somente se, for um número real.

Seja C a única circunferência que passa pelos pontos z₁ = 1, z₂ = -3i e z₃ = -7 + 4i  do plano complexo.

Assim sendo, determine todos os pontos do plano complexo cuja parte real é igual  a –1  e que estão sobre a circunferência C. 

   25. (UFMG) 2002 - Observe esta figura: 

 

Nessa figura, OP = 2 e OQ = 4.

Sejam z e w, respectivamente, os números complexos representados geometricamente pelos pontos  P e Q.  

Considerando esses dados, escreva o número complexo z¹¹ / i.w⁵ na forma a + bi, em que a e b são números reais.

   26. (UEFS) O valor da expressão E = x^-1 + x², para x = 1 - i, é:

a) -3i      b) 1 – i      c) 5/2 + (5/2)i      d) 5/2 - (3/2)i       e) ½ - (3/2)i

   27. (UEFS) Simplificando-se a expressão E = i⁷ + i⁵ + ( i³ + 2i⁴ )² , obtêm-se:

a) -1 + 2i      b) 1 + 2i      c) 1 - 2i      d) 3 - 4i      e) 3 + 4i

   28. (UEFS) Se m - 1 + ni = (3 + i).(1 + 3i), então m e n são respectivamente:

a) 1 e 10      b) 5 e 10       c) 7 e 9      d) 5 e 9      e) 0 e -9

   29. (UEFS) A soma de um número complexo z com o triplo do seu conjugado é igual a -8 - 6i. O módulo de z é:

a) Ö13      b) Ö7       c) 13      d) 7      e) 5 

   30. (FESP/UPE) Seja  z = 1 + i, onde i é a unidade imaginária. Podemos afirmar que z⁸ é igual a:

a) 16      b) 161      c) 32      d) 32i      e) 32 + 16i 

    31. (UCSal) Sabendo que (1 + i)² = 2i, então o valor da expressão y = (1 + i)⁴⁸ - (1 + i)⁴⁹ é:

a) 1 + i       b) -1 + i       c) 2²⁴ . i       d) 2⁴⁸ . i       e) -2²⁴ . i 

Resposta:

1)D  2)E 3)D  4)E 5)B  6)C 7)B  8)D  9) A  10) B
11) -3 - i  12) -3 + 18i  13) 4 + 3i  14) 3/2  15) -2 + 18i  16) i  17) 3  18) 1 + 2i
19) 50   20) 32i  21) -1 - i   24) –1 + 4i e -1 – 4i  26) B  27) D  28) A
29) A   30) A   31) E

Números Complexos - Direto ao assunto (Aula 4 de 4)

Números Complexos - Matemática - Direto ao assunto (Aula 3 de 4)

Números Complexos - Direto ao assunto (aula 2 de 4)

Números Complexos - Parte 1.wmv

Números complexos - aula 2 - parte 1

Números complexos - parte 1

Exercícios

Agora é a sua vez: Teste seus conhecimentos!!!

01. O produto (5 + 7i) (3 - 2i) vale:

a) 1 + 11i

b) 1 + 31i

c) 29 + 11i

d) 29 - 11i

e) 29 + 31i

RESPOSTA: C

02. Se f(z) = z2 - z + 1, então f(1 - i) é igual a:

a) i

b) -i + 1

c) i - 1

d) i + 1

e) -i

RESPOSTA: C

03. (FUVEST) Sendo i a unidade imaginária (i2 = -1) pergunta-se: quantos números reais a existem para os quais (a + 1)4 é um número real?

a) 1

b) 2

c) 3

d) 4

e) infinitos

RESPOSTA: C

04. Sendo i a unidade imaginária o valor de i10 + i-100 é:

a) zero

b) i

c) -i

d) 1

e) -1

RESPOSTA: A

05. Sendo i a unidade imaginária, (1 - i )-2 é igual a:

a) 1

b) -i

c) 2i

d) -i/2

e) i/2

RESPOSTA: E

06. A potência (1 - i )16 equivale a:

a) 8

b) 16 - 4i

c) 16 - 16i

d) 256 - 16i

e) 256

RESPOSTA: E

07. Se os números complexos z1 = 2 - i e z2 = x + 1, x real e positivo, são tais que |z1 . z2|2 = 10 então x é igual a:

a) 5

b) 4

c) 3

d) 2

e) 1

RESPOSTA: E

08. O módulo do complexo cos a - i . sen a é:

a) -1

b) -i

c) i

d) i4

e) i5

RESPOSTA: D

09. Calcular as raízes quadradas do número complexo 5 - 12i.

RESOLUÇÃO: 3 - 2i; -3 + 2i

10. Achar o conjunto-verdade, em R, da equação x8 - 17x4 + 16 = 0.

RESOLUÇÃO: V = {1, i, -1, -i, 2, 2i, -2, -2i}

Argumento

Argumento de um número complexo

 

    Os números complexos são uma extensão do conjunto dos números reais. Na verdade, número complexo é um par ordenado de números reais (a, b). Escrito na forma normal, o par ordenado (a, b) fica z = a + bi. Representando esse número complexo no plano de Argand-Gauss, teremos:

 

     O segmento de reta OP é chamado de módulo do número complexo. O arco  formado entre o eixo horizontal positivo e o segmento OP, no sentido anti-horário, é chamado de argumento de z. Observe a figura abaixo para determinarmos as características do argumento de z.

  

       No triângulo retângulo formado, podemos afirmar que:

  

      Podemos constatar, também, que: 

 

      Ou 

 

      Exemplo 1. Dado o número complexo z = 2 + 2i, determine o módulo e o argumento de z.

      Solução: Pelo número complexo z = 2 + 2i, sabemos que a = 2 e b = 2. Segue que: 

 

 

     Exemplo 2. Determine o argumento do número complexo z = – 3 – 4i.
Solução: Para determinar o argumento de z, precisamos conhecer o valor de |z|. Assim, como a = – 3 e b = – 4, teremos:   

 

      Nos casos em que o argumento não for um ângulo notável, é preciso determinar o valor de sua tangente, como feito no exemplo anterior, para só depois podermos afirmar quem é o argumento. Exemplo 3. Dado o número complexo z = – 6i, determine o argumento de z.
Solução: Vamos calcular o valor do módulo de z. 

 

Potência de i

Potência i

     Os números complexos são identificados por z = a + bi, onde a é a parte real e b a parte imaginária. A letra i acompanha a parte imaginária e dependo do valor de sua potência ela irá assumir um valor que irá facilitar vários cálculos.

i ⁰ = 1, pois todo número ou letra elevando à zero é um.
i ¹ = i, pois todo número elevado a 1 é ele mesmo.
i ² = -1, a partir dessa potência que as outras irão derivar, veja:
i ³ = i² . i = -1 . i = - i
i ⁴ = i² . i² = -1 . (-1) = 1
i ⁵ = i⁴ . i = 1 . i = i
i ⁶ = i⁴ . i² = 1 . (-1) = -1.
i ⁷ = i⁴ . i³ = 1 . (-i) = - i.

     E assim por diante.

    Para descobrir, por exemplo, qual era o valor da potência i ²⁴³, basta observar o seguinte: nas potências acima elas repetem-se de 4 em 4, então basta dividirmos 243 por 4, o resto será 3 então i²⁴³ será o mesmo que i³, portanto i²⁴³ = - i.

     Podemos concluir que i ⁿ = i^r, onde r é o resto da divisão.

Módulo

Plano de Argand-Gauss

     A cada número complexo z = a + bi, podemos associar um ponto P no plano cartesiano. No complexo podemos representar a parte real por um ponto no eixo real, e a parte imaginária por um ponto no eixo vertical, denominado eixo imaginário.
     A este ponto P, correspondente ao complexo z = a +bi, chamamos de imagem ou afixo de z. Observe a representação da interpretação geométrica dos números complexos: 

 

     Atualmente, o plano dos números complexos é conhecido como plano de Argand-Gauss.

   Com base no plano representado vamos calcular a distância p (letra grega: rô), entre os pontos O e P. Observe que basta aplicarmos o Teorema de Pitágoras no triângulo retângulo, dessa forma temos:

 

     O módulo de z é representado pela grandeza p, mas também pode ser representado por |z|.

     O ângulo Ө (0 ≤ Ө < 2π), formado pelo eixo real e a reta do segmento OP, é chamado de argumento de z (z ≠ 0) e é indicado por Arg(z). Baseado nessas definições podemos estabelecer as seguintes relações na interpretação geométrica dos complexos:

 

     Exemplo
     Calcule o módulo e o argumento do número complexo z = 1 + 2i.

     Módulo
a = 1 e b = 2 

 

 

 

Argumento
Ө = Arg(z)

 

   Portanto, o argumento de z é o arco cuja tangente é 2.           

   Veja como ficaria o gráfico representativo do número complexo z = 1 + 2i. 

Divisão de números complexos

    Ao dividirmos dois números complexos devemos escrevê-los em forma de fração e multiplicarmos o numerador e o denominador pelo conjugado do denominador, veja como:

     Dado dois números complexos z ₁ e z₂, para efetuarmos a divisão dos dois devemos seguir a seguinte regra: 

z₁ : z₂ = z₁  .  
               z₂       

   De uma forma geral podemos demonstrar a divisão de dois números complexos por:

      Dado z1 = a + bi e z2 = c + di a divisão de z1 : z2 será: