Argumento

Argumento de um número complexo

 

    Os números complexos são uma extensão do conjunto dos números reais. Na verdade, número complexo é um par ordenado de números reais (a, b). Escrito na forma normal, o par ordenado (a, b) fica z = a + bi. Representando esse número complexo no plano de Argand-Gauss, teremos:

 

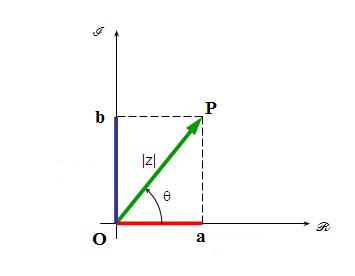
     O segmento de reta OP é chamado de módulo do número complexo. O arco  formado entre o eixo horizontal positivo e o segmento OP, no sentido anti-horário, é chamado de argumento de z. Observe a figura abaixo para determinarmos as características do argumento de z.

  

       No triângulo retângulo formado, podemos afirmar que:

  

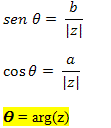
      Podemos constatar, também, que: 

 

      Ou 

 

      Exemplo 1. Dado o número complexo z = 2 + 2i, determine o módulo e o argumento de z.

      Solução: Pelo número complexo z = 2 + 2i, sabemos que a = 2 e b = 2. Segue que: 

 

 

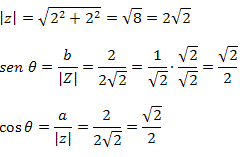
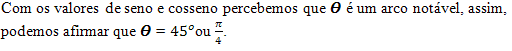
     Exemplo 2. Determine o argumento do número complexo z = – 3 – 4i.
Solução: Para determinar o argumento de z, precisamos conhecer o valor de |z|. Assim, como a = – 3 e b = – 4, teremos:   

 

      Nos casos em que o argumento não for um ângulo notável, é preciso determinar o valor de sua tangente, como feito no exemplo anterior, para só depois podermos afirmar quem é o argumento. Exemplo 3. Dado o número complexo z = – 6i, determine o argumento de z.
Solução: Vamos calcular o valor do módulo de z.