ESFERA

CONCEITO

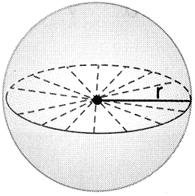
Consideramos um ponto O e um segmento de medida r. Chama-se esfera de centro O e raio r o conjunto dos pontos P do espaço , tais que a distância OP seja menor ou igual a r.

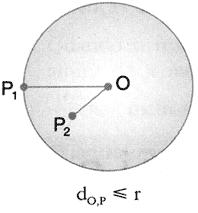
A esfera é o sólido de revolução gerado pela rotação completa de um semicírculo em torno de um eixo que contém um diâmetro.

SUPERFÍCIE ESFÉRICA

Superfície esférica de centro O e raio r é o conjunto dos pontos P do espaço que distam r do ponto o.

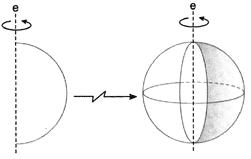
A superfície gerada pela rotação de uma semicircunferência em torno de um eixo que contém o diâmetro é uma superfície esférica.

ELEMENTOS DA ESFERA

Considerando a superfície de uma esfera de eixo e, temos:
a) Pólos são as interseções da superfície com o eixo;
b) Equador é a seção (circunferência) perpendicular ao eixo, pelo centro da superfície;

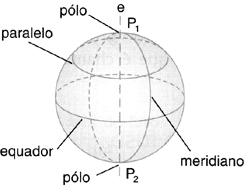
c) Paralelo é qualquer seção (circunferência) perpendicular ao eixo;
d) Meridiano é qualquer seção (circunferência) cujo plano passa pelo eixo.

SEÇÃO DA ESFERA

Toda seção plana de uma esfera é um círculo.
Sendo r o raio da esfera, d a distância do plano secante ao centro e s o raio da seção, vale a relação

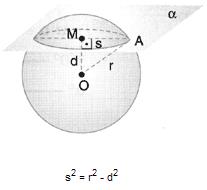
Se o plano secante passa pelo centro da esfera, temos como seção um círculo máximo da esfera.

ÁREA DA ESFERA 

A área de uma superfície esférica de raio r é igual a 4r².
A = 4r²

VOLUME DA ESFERA

Aplicação
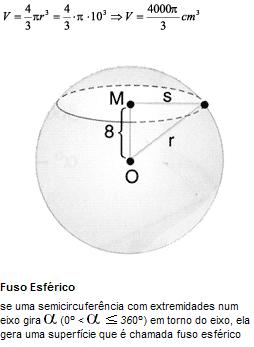
Uma esfera é secionada por um plano a 8cm do centro; a seção obtida tem área 36cm2.
Determinar a área da superfície da esfera e seu volume.
Solução:
Inicialmente, devemos considerar a área da seção:
36 = . s² →s = 6cm
s² = r² – d^2→ 6² = r² – 8² r = 10cm
A = 4r² = 4 . 10² →A = 400cm2

VOLUME DA ESFERA



Aplicação


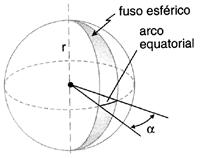
ÁREA DO FUSO

Note que, quanto maior for o ângulo, maior será o fuso correspondente; a área do fuso é diretamente proporcional a .
Assim, podemos estabelecer as seguintes regras de três simples:



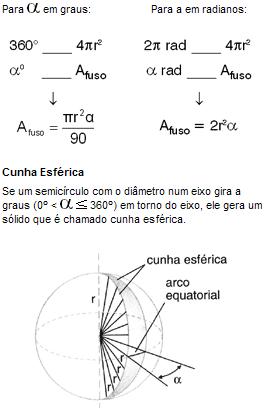
VOLUME DA CUNHA

Note que quanto maior for o ângulo, maior será o volume da cunha correspondente; o volume da cunha é diretamente proporcional a .
Assim, podemos estabelecer as seguintes regras de três simples:

QUESTÕES RESOLVIDAS:

01.A localização de um ponto qualquer na superfície da Terra (considerada como uma esfera) é feita, em geral, a partir de duas coordenadas, sendo uma delas a latitude – que é o ângulo (em grau) entre o plano que contém a linha do equador e o segmento que une o centro da esfera ao ponto em questão.

Sabe-se que as cidades de Porto Alegre e de Macapá situam-se, praticamente, no mesmo meridiano. Considere que a cidade de Macapá (ponto M) localiza- se bem próximo da linha do equador (latitude = 0°02’20" ao norte); que a latitude de Porto Alegre (ponto P) é de 30° 01’59" ao sul e que o valor do diâmetro da Terra é de 12 750 quilômetros. Veja figura a seguir:

 

Tendo em vista tais considerações, pode-se afirmar que a distância, em quilômetro, entre as duas cidades é de aproximadamente:

A)	2 300
B)	3 300  x
C)	4 600
D)	6 600
E)	9 000

02. A tira seguinte mostra o Cebolinha tentando levantar um haltere, que é um aparelho feito de ferro, composto de duas esferas acopladas a um bastão cilíndrico.

Suponha que cada esfera tenha 10,5cm de diâmetro e que o bastão tenha 50cm de comprimento e diâmetro da base medindo 1,4cm. Se a densidade do ferro é 7,8g/cm³, quantos quilogramas, aproximadamente, o Cebolinha tentava levantar? (Use: p = 22/7)

A)	18
B)	16
C)	15
D)	12
E)	10  x